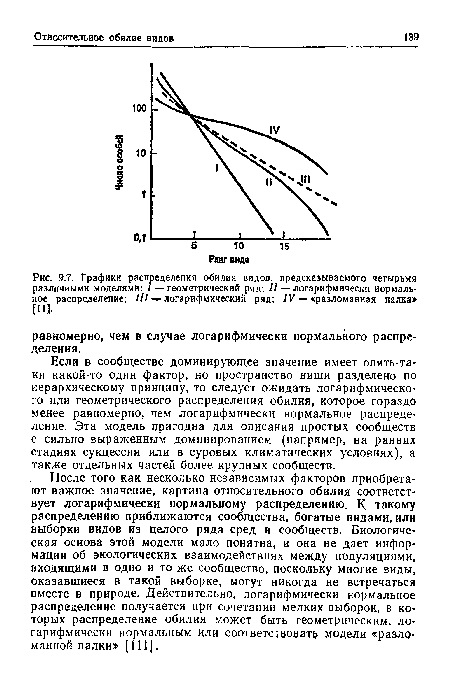
/ — геометрический ряд; II — логарифмически нормальное распределение; III — логарифмический ряд; IV — «разломанная палка» [И].
Эти различные модели образуют семейство взаимно пересекающихся кривых, в чем легко убедиться, если одновременно построить графики зависимости предсказываемых распределений логарифмов обилия от ранга видов (рис. 9.7). Когда динамика сообщества зависит главным образом от какого-либо одного фактора, пригодна модель «разломанной палки» как статистически реалистичное выражение равномерного распределения. Логарифмический ряд — это статистическое выражение неравномерного процесса, при котором возможен преимущественный захват ниш и идеальная форма которого описывается геометрической прогрессией [209]. Промежуточное положение между этими крайностями занимает логарифмически нормальное распределение, возникающее в среде, подверженной случайным, флуктуациям, и (или) когда в динамике обширной ассамблеи видов важную роль играют несколько факторов. Соответствие распределения обилия той или иной из этих моделей, по всей вероятности, выражает нечто существенное, касающееся данной группы видов. Вместо того чтобы выбирать модель, которая лучше всего описывает относительные обилия видов, следует выяснить, в каких случаях и почему они в данном сообществе приближаются к одному из рассмотренных распределений.
Вернуться к оглавлению